多元线性回归

在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。因此多元线性回归比一元线性回归的实用意义更大。

多维特征

多元线性回归含有多个变量的模型，模型中的特征为 $\left( {x_{1}},{x_{1}},...,{x_{n}} \right)$。

增添更多特征后，引入一系列新的注释：

$n$ 代表特征的数量

${x^{\left( i \right)}}$ 代表第  $i$ 个训练实例，是特征矩阵中的第 $i$ 行，是一个向量（vector）。

${x}_{j}^{\left( i \right)}$ 代表特征矩阵中第 $i$ 行的第 $j$ 个特征，也就是第 $i$ 个训练实例的第 $j$ 个特征。

支持多变量的假设 $h$ 表示为：$h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}$，

这个公式中有 $n+1$ 个参数和 $n$ 个变量，为了使公式简化一些，引入 $x_{0}=1$，则公式转化为：

$h_{\theta} \left( x \right)={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}$

此时模型中的参数是一个  $n+1$ 维的向量，任何一个训练实例也都是  $n+1$ 维的向量，特征矩阵 X 的维度是 $m*(n+1)$。

因此公式简化为：$h_{\theta} \left( x \right)={\theta^{T}}X$，其中上标 $T$ 代表矩阵转置。

多变量梯度下降

与单变量线性回归类似，在多变量线性回归中，我们构建一个代价函数，是所有建模误差的平方和，即：$J\left( {\theta_{0}},{\theta_{1}}...{\theta_{n}} \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}}$ ，

其中：$h_{\theta}\left( x \right)=\theta^{T}X={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}$ ，

我们的目标是要找出使得代价函数最小的一系列参数。 多变量线性回归的批量梯度下降算法为：

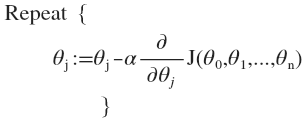
即：

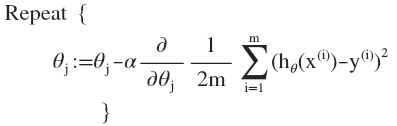
求导数后得到：

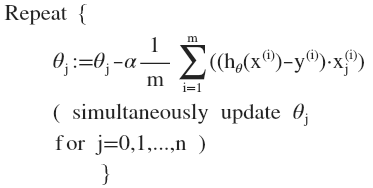
当 $n>=1$ 时，$ {{\theta }_{0}}:={{\theta }_{0}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}x_{0}^{(i)}$

${{\theta }_{1}}:={{\theta }_{1}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}x_{1}^{(i)}$

${{\theta }_{2}}:={{\theta }_{2}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}x_{2}^{(i)}$

我们开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

代码示例：

计算代价函数 $J\left( \theta  \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}}$  

其中：${h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}$

Python 代码：

def computeCost(X, y, theta):

    inner = np.power(((X * theta.T) - y), 2)

    return np.sum(inner) / (2 * len(X))

梯度下降算法 - 学习率

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

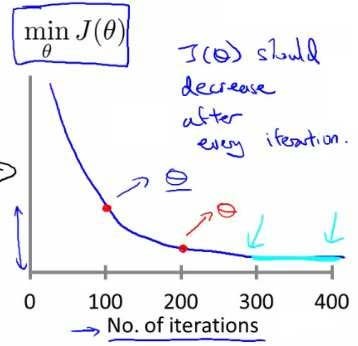
也有一些自动测试是否收敛的方法，例如将代价函数的变化值与某个阀值（例如0.001）进行比较。

梯度下降算法的每次迭代受到学习率的影响，如果学习率 $\alpha$ 过小，则达到收敛所需的迭代次数会非常高；如果学习率 $\alpha$ 过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

考虑尝试些学习率：$\alpha=0.01，0.03，0.1，0.3，1，3，10$