卷积神经网络（CNN）卷积层

卷积神经网络的名字来源于“卷积”运算。在卷积神经网络中，卷积的主要目的是从输入图像中提取特征。通过使用输入数据中的小方块来学习图像特征，卷积保留了像素间的空间关系。

卷积定义

在泛函分析中，卷积（ convolution ）是一种函数的定义 。 它是通过两个函数 f 和 g 生成第三个函数的一种数学算子，表征函数 f与 g 经过翻转和平移的重叠部分的面积 。

微积分中卷积的表达式为：$S(t)=∫x(t−a)w(a)da$

离散形式是：$s(t) = \sum\limits_ax(t-a)w(a)$

这个式子如果用矩阵表示可以为：$s(t)=(X∗W)(t)$  其中星号表示卷积。

如果是二维的卷积，则表示式为：

$s(i,j)=(X*W)(i,j) = \sum\limits_m \sum\limits_n x(i-m,j-n) w(m,n)$

在CNN中，虽然我们也是说卷积，但是我们的卷积公式和严格意义数学中的定义稍有不同,比如对于二维的卷积，定义为：

$s(i,j)=(X*W)(i,j) = \sum\limits_m \sum\limits_n x(i+m,j+n) w(m,n)$

其中，我们叫W为我们的卷积核，而X则为我们的输入。如果X是一个二维输入的矩阵，而W也是一个二维的矩阵。但是如果X是多维张量，那么W也是一个多维的张量。

卷积层（Convolutional Layer）

对图像卷积，其实就是对输入的图像的不同局部的矩阵和卷积核矩阵各个位置的元素相乘，然后相加得到

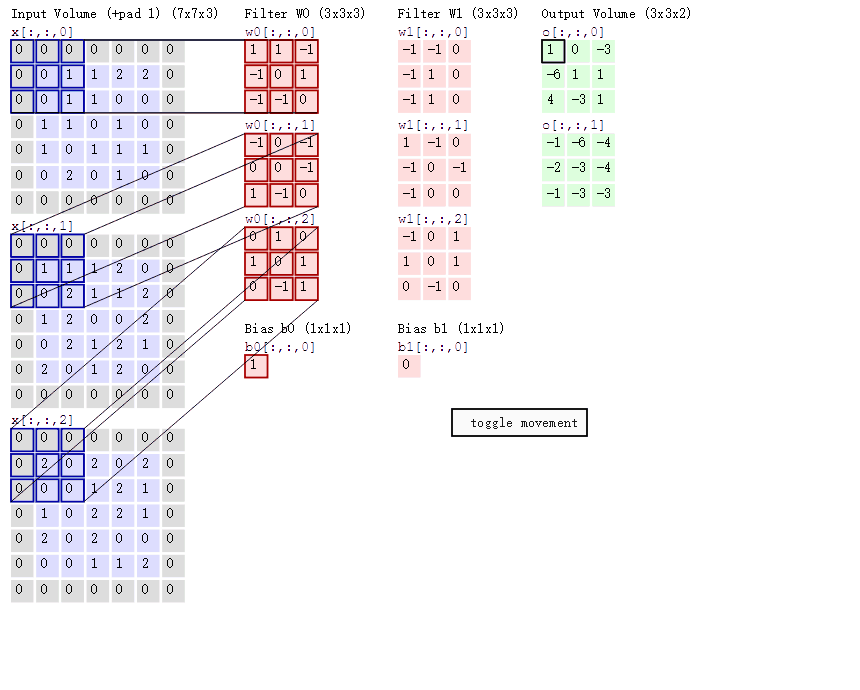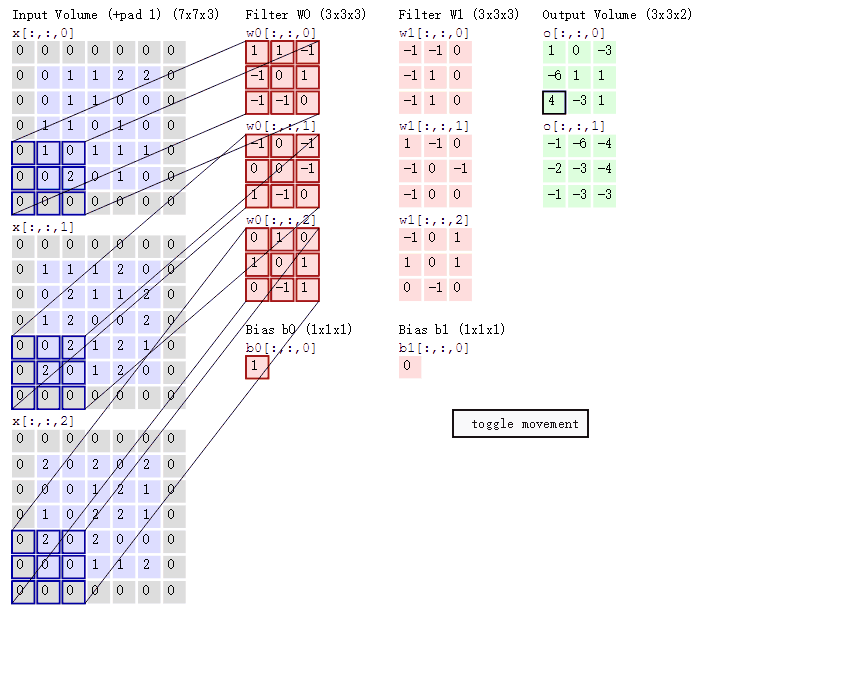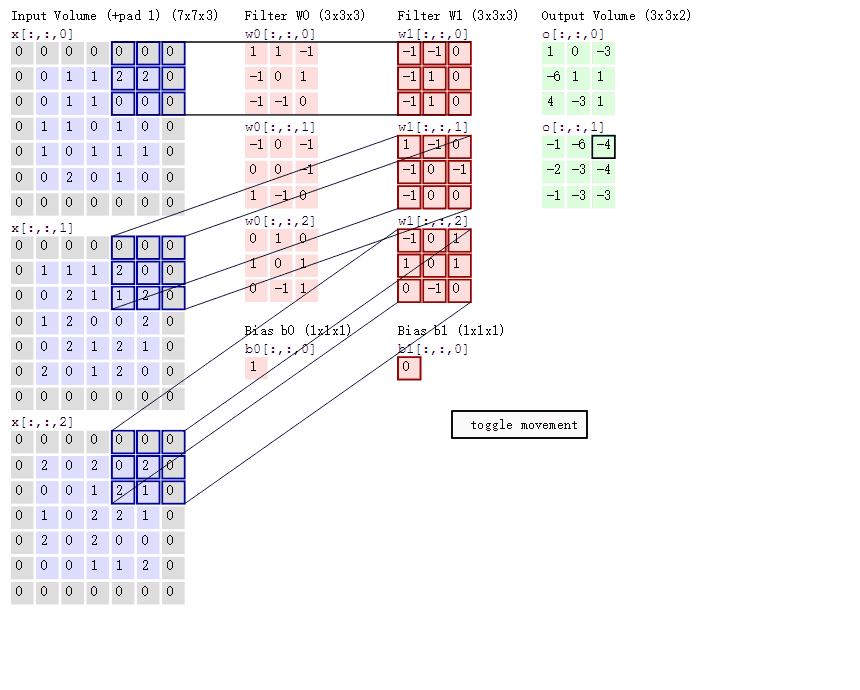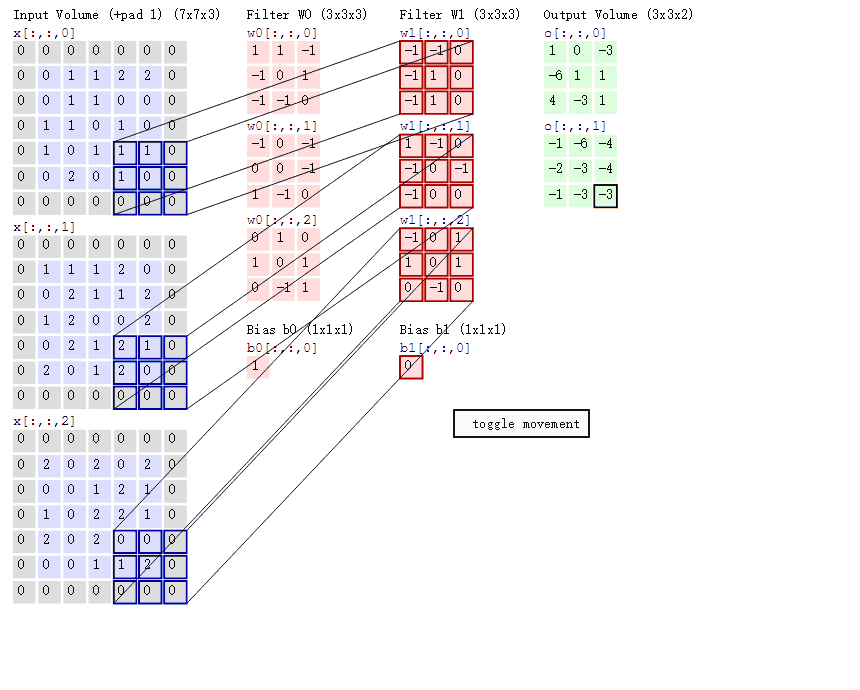
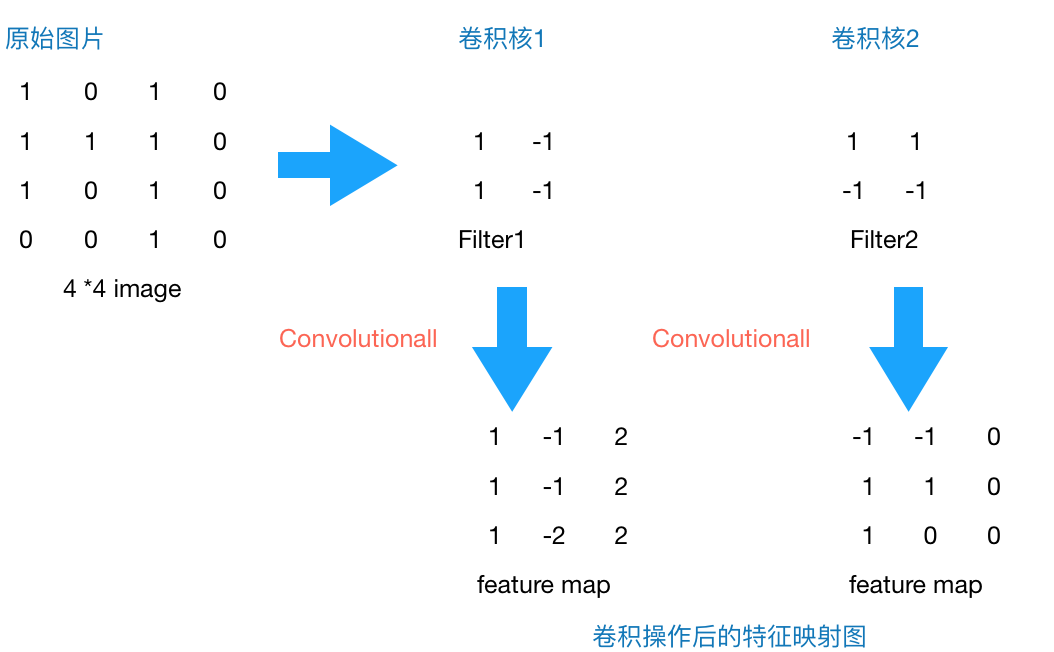
原始图片是一张灰度图片,每个位置表示的是像素值，0表示白色，1表示黑色，（0，1）区间的数值表示灰色。对于这个4*4的图像，我们采用两个2*2的卷积核来计算。设定步长为1，即每次以2*2的固定窗口往右滑动一个单位。以第一个卷积核filter1为例，计算过程如下：

1 feature_map1(1,1) = 1*1 + 0*(-1) + 1*1 + 1*(-1) = 1 

2 feature_map1(1,2) = 0*1 + 1*(-1) + 1*1 + 1*(-1) = -1 

3 ......

4 feature_map1(3,3) = 1*1 + 0*(-1) + 1*1 + 0*(-1) = 2

feature_map1(1,1)表示在通过第一个卷积核计算完后得到的feature_map的第一行第一列的值，随着卷积核的窗口不断的滑动，我们可以计算出一个3*3的feature_map1;同理可以计算通过第二个卷积核进行卷积运算后的feature_map2，那么这一层卷积操作就完成了。feature_map尺寸计算公式：[ (原图片尺寸 -卷积核尺寸)/ 步长 ] + 1。

卷积核

卷积层的功能是对输入数据进行特征提取，其内部包含多个卷积核，组成卷积核的每个元素都对应一个权重系数和一个偏差量（bias vector），类似于一个前馈神经网络的神经元（neuron）。卷积层内每个神经元都与前一层中位置接近的区域的多个神经元相连，区域的大小取决于卷积核的大小，卷积核在工作时，会有规律地扫过输入特征，对输入特征做矩阵元素乘法求和并叠加偏差量

  为偏差量，  和  表示第  层的卷积输入和输出，也被称为特征图（feature map），  为  的尺寸，这里假设特征图长宽相同。  对应特征图的像素，  为特征图的通道数，  、  和  是卷积层参数，对应卷积核大小、卷积步长（stride）和填充（padding）层数。

实际上，卷积神经网络在训练过程中会自己学习这些过滤器的值（尽管在训练过程之前我们仍需要指定诸如过滤器数目、大小，网络框架等参数）。我们拥有的过滤器数目越多，提取的图像特征就越多，我们的网络在识别新图像时效果就会越好。对于卷积后的输出，一般会通过ReLU激活函数，将输出的张量中的小于0的位置对应的元素值都变为0。

卷积层参数

卷积层参数包括卷积核大小、步长和填充，三者共同决定了卷积层输出特征图的尺寸，是卷积神经网络的超参数 。

卷积核大小可以指定为小于输入图像尺寸的任意值，卷积核越大，可提取的输入特征越复杂 。

卷积步长定义了卷积核相邻两次扫过特征图时位置的距离，卷积步长为1时，卷积核会逐个扫过特征图的元素，步长为n时会在下一次扫描跳过n-1个像素 。

填充是在特征图通过卷积核之前人为增大其尺寸以抵消计算中尺寸收缩影响的方法。常见的填充方法为按0填充和重复边界值填充（replication padding）。填充依据其层数和目的可分为四类：

• 有效填充（valid padding）：即完全不使用填充，卷积核只允许访问特征图中包含完整感受野的位置。输出的所有像素都是输入中相同数量像素的函数。使用有效填充的卷积被称为“窄卷积（narrow convolution）”，窄卷积输出的特征图尺寸为(L-f)/s+1。
• 相同填充/半填充（same/half padding）：只进行足够的填充来保持输出和输入的特征图尺寸相同。相同填充下特征图的尺寸不会缩减但输入像素中靠近边界的部分相比于中间部分对于特征图的影响更小，即存在边界像素的欠表达。使用相同填充的卷积被称为“等长卷积（equal-width convolution）”。
• 全填充（full padding）：进行足够多的填充使得每个像素在每个方向上被访问的次数相同。步长为1时，全填充输出的特征图尺寸为L+f-1，大于输入值。使用全填充的卷积被称为“宽卷积（wide convolution）”
• 任意填充（arbitrary padding）：介于有效填充和全填充之间，人为设定的填充，较少使用。

卷积层激励函数（activation function）

卷积层中包含激励函数以协助表达复杂特征，其表示形式如下 ：

类似于其它深度学习算法，卷积神经网络通常使用线性整流单元（Rectified Linear Unit, ReLU），其它类似ReLU的变体包括有斜率的ReLU（Leaky ReLU, LReLU）、参数化的ReLU（Parametric ReLU, PReLU）、随机化的ReLU（Randomized ReLU, RReLU）、指数线性单元（Exponential Linear Unit, ELU）等。在ReLU出现以前，Sigmoid函数和双曲正切函数（hyperbolic tangent）是常用的激励函数。

激励函数操作通常在卷积核之后，一些使用预激活（preactivation）技术的算法将激励函数置于卷积核之前。在一些早期的卷积神经网络研究，例如LeNet-5中，激励函数在池化层之后 。

ReLU 全称为修正线性单元（Rectified Linear Units），是一种非线性操作。 其输出如下图所示：

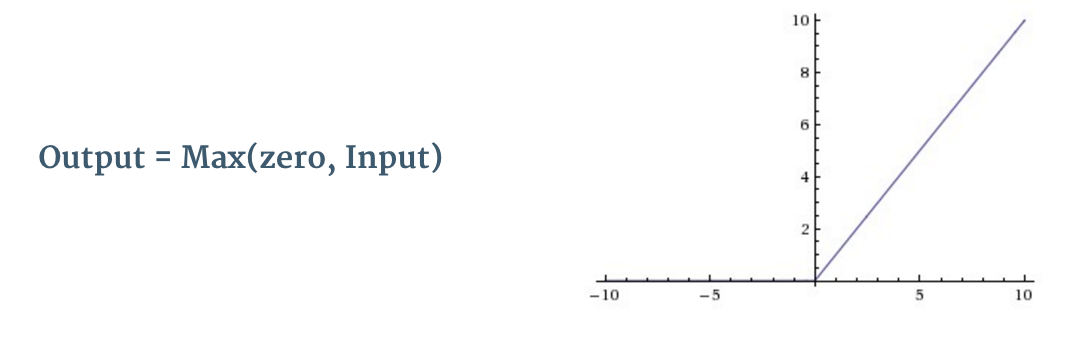
ReLU 是一个针对元素的操作（应用于每个像素），并将特征映射中的所有负像素值替换为零。ReLU 的目的是在卷积神经网络中引入非线性因素，因为在实际生活中我们想要用神经网络学习的数据大多数都是非线性的（卷积是一个线性运算 —— 按元素进行矩阵乘法和加法，所以我们希望通过引入 ReLU 这样的非线性函数来解决非线性问题）。

激励层的实践经验：

1. 不要用sigmoid
2. 首先试RELU，因为快，但要小心点
3. 如果2失效，请用Leaky ReLU或者Maxout
4. 某些情况下tanh倒是有不错的结果，但是很少