Neo4j图论基础知识

图论(Graph Theory)是离散数学的一个分支，是一门研究图(Graph)的学问。

图是用来对对象之间的成对关系建模的数学结构，由"节点"或"顶点"(Vertex）以及连接这些顶点的"边"（Edge）组成。

值得注意的是，图的顶点集合不能为空，但边的集合可以为空。图可能是无向的，这意味着图中的边在连接顶点时无需区分方向。否则，称图是有向的。

图的定义

图G是由两个集合V和E组成(记做 G = (V, E))：

V = {v1,v2,v3,...vn,} 是由G的结点(vertex)组成的集合

E = {e1,e2,e3,...en} 是由连接两个结点的边(edge)组成的集合

(无向图)若边e(唯一的边)连接结点v1和v2, 则表示为 e = (v1,v2)或 e = (v2,v1)，表示连接结点v1和结点v2的边

(有向图)若边e(唯一的边)连接有序结点对v1和v2, 则表示为 e = (v1,v2)，

表示一条从结点v1到结点v2的边

(有向图和无向图)G中的一条边连接结点v1和结点v2，则称结点v1和结点v2相关联，结点v1和结点v2是相邻结点

(有向图和无向图)一般情况下，E 和 V 都是有限的集合，且 V 为非空

图的表达形式

邻接矩阵：1 表示相连接，0 表示不相连。

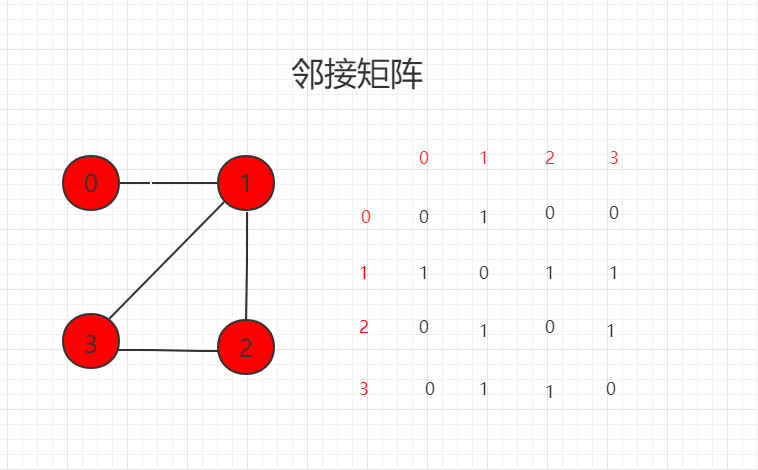
邻接表：只表达和顶点相连接的顶点信息

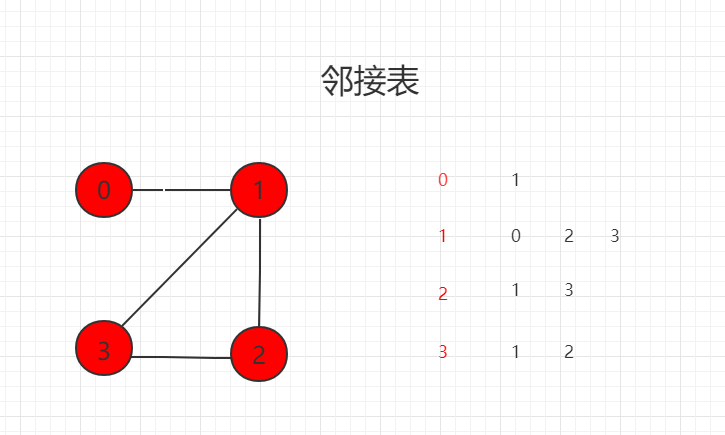
邻接表适合表示稀疏图 (Sparse Graph)

邻接矩阵适合表示稠密图 (Dense Graph)